Simple check of a sample against 80 distributions
Who ever wanted to check a sample of measurements against different distributions… Here is a quite simple way to do so by using python scipy. We have for example a random sample of 500 values generated with the following command (the complete script can be downloaded at https://github.com/andre-dietrich/distribution-check):
import scipy.stats
sample = scipy.stats.halflogistic(1,1).rvs(500)The following picture shows a histogram of our sample:
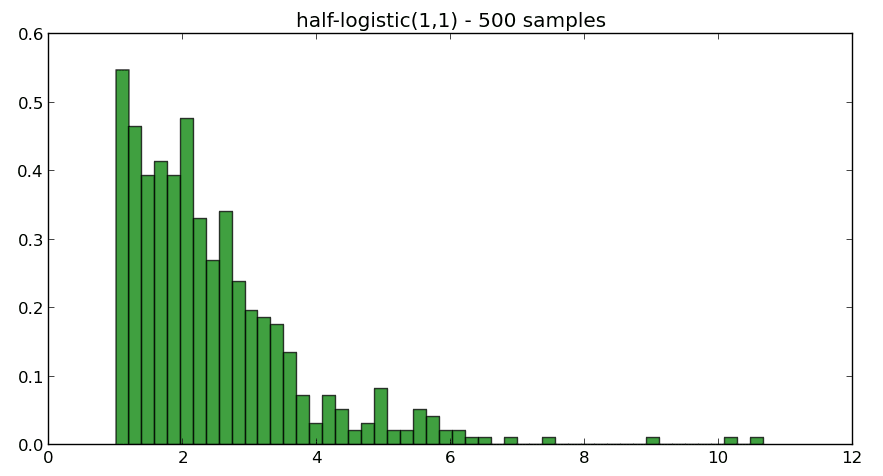
Of course, we know that the distribution is half-logistic, but is it also possible to determine the probability distribution afterwards? Scipy already includes all necessary stuff, firstly here is a list of some available distributions:
cdfs = [
"norm", #Normal (Gaussian)
"alpha", #Alpha
"anglit", #Anglit
"arcsine", #Arcsine
"beta", #Beta
"betaprime", #Beta Prime
"bradford", #Bradford
"burr", #Burr
"cauchy", #Cauchy
"chi", #Chi
"chi2", #Chi-squared
"cosine", #Cosine
"dgamma", #Double Gamma
"dweibull", #Double Weibull
"erlang", #Erlang
"expon", #Exponential
"exponweib", #Exponentiated Weibull
"exponpow", #Exponential Power
"fatiguelife", #Fatigue Life (Birnbaum-Sanders)
"foldcauchy", #Folded Cauchy
"f", #F (Snecdor F)
"fisk", #Fisk
"foldnorm", #Folded Normal
"frechet_r", #Frechet Right Sided, Extreme Value Type II
"frechet_l", #Frechet Left Sided, Weibull_max
"gamma", #Gamma
"gausshyper", #Gauss Hypergeometric
"genexpon", #Generalized Exponential
"genextreme", #Generalized Extreme Value
"gengamma", #Generalized gamma
"genlogistic", #Generalized Logistic
"genpareto", #Generalized Pareto
"genhalflogistic", #Generalized Half Logistic
"gilbrat", #Gilbrat
"gompertz", #Gompertz (Truncated Gumbel)
"gumbel_l", #Left Sided Gumbel, etc.
"gumbel_r", #Right Sided Gumbel
"halfcauchy", #Half Cauchy
"halflogistic", #Half Logistic
"halfnorm", #Half Normal
"hypsecant", #Hyperbolic Secant
"invgamma", #Inverse Gamma
"invnorm", #Inverse Normal
"invweibull", #Inverse Weibull
"johnsonsb", #Johnson SB
"johnsonsu", #Johnson SU
"laplace", #Laplace
"logistic", #Logistic
"loggamma", #Log-Gamma
"loglaplace", #Log-Laplace (Log Double Exponential)
"lognorm", #Log-Normal
"lomax", #Lomax (Pareto of the second kind)
"maxwell", #Maxwell
"mielke", #Mielke's Beta-Kappa
"nakagami", #Nakagami
"ncx2", #Non-central chi-squared
# "ncf", #Non-central F
"nct", #Non-central Student's T
"pareto", #Pareto
"powerlaw", #Power-function
"powerlognorm", #Power log normal
"powernorm", #Power normal
"rdist", #R distribution
"reciprocal", #Reciprocal
"rayleigh", #Rayleigh
"rice", #Rice
"recipinvgauss", #Reciprocal Inverse Gaussian
"semicircular", #Semicircular
"t", #Student's T
"triang", #Triangular
"truncexpon", #Truncated Exponential
"truncnorm", #Truncated Normal
"tukeylambda", #Tukey-Lambda
"uniform", #Uniform
"vonmises", #Von-Mises (Circular)
"wald", #Wald
"weibull_min", #Minimum Weibull (see Frechet)
"weibull_max", #Maximum Weibull (see Frechet)
"wrapcauchy", #Wrapped Cauchy
"ksone", #Kolmogorov-Smirnov one-sided (no stats)
"kstwobign"] #Kolmogorov-Smirnov two-sided test for Large NAnd finally, there are only two things, which we have to do… fitting our set of sample against every probability distribution and applying the “Kolmogorov-Smirnof one sided test” as follows:
for cdf in cdfs:
#fit our data set against every probability distribution
parameters = eval("scipy.stats."+cdf+".fit(sample)");
#Applying the Kolmogorov-Smirnof one sided test
D, p = scipy.stats.kstest(sample, cdf, args=parameters);
#pretty-print the results
print cdf.ljust(16) + ("p: "+str(p)).ljust(25)+"D: "+str(D);Running this example, we get the following result:
norm p: 4.32985784116e-07 D: 0.123361363632
alpha p: 0.0 D: nan
anglit p: 1.57405644075e-09 D: 0.14414705595
arcsine p: 0.0 D: 0.194487444742
beta p: 0.17194522643 D: 0.0492004317884
betaprime p: 0.0 D: nan
bradford p: 2.6871305181e-10 D: 0.150085923622
burr p: 0.0 D: nan
cauchy p: 0.0 D: nan
chi p: 0.202823098481 D: 0.0475053082334
chi2 p: 0.0 D: 0.258
cosine p: 1.33185751316e-08 D: 0.136622959885
dgamma p: 1.99526513089e-08 D: 0.135150952901
dweibull p: 9.10639612606e-08 D: 0.129470516829
erlang p: 1.55989546051e-05 D: 0.108
expon p: 1.55989546051e-05 D: 0.108
exponweib p: 1.55989546051e-05 D: 0.108
exponpow p: 0.00738341390149 D: 0.0744818772737
fatiguelife p: 2.64361865732e-10 D: 0.150139654368
foldcauchy p: 0.0 D: nan
f p: 0.0 D: nan
fisk p: 0.0 D: nan
foldnorm p: 0.0195268210697 D: 0.0676853081311
frechet_r p: 1.55989546051e-05 D: 0.108
frechet_l p: 0.0 D: 0.250852727712
gamma p: 0.064713393752 D: 0.0582325521395
gausshyper p: 2.6871305181e-10 D: 0.150085923622
genexpon p: 0.793140816507 D: 0.0290362909155
genextreme p: 0.0 D: 0.250852727712
gengamma p: 1.55989546051e-05 D: 0.108
genlogistic p: 0.197774458464 D: 0.0477678936548
genpareto p: 0.0 D: nan
genhalflogistic p: 1.11022302463e-15 D: 0.186514196604
gilbrat p: 0.0 D: 0.244376114481
gompertz p: 0.104396819147 D: 0.0540007747394
gumbel_l p: 0.0 D: 0.266977935937
gumbel_r p: 0.191127509048 D: 0.0481217433314
halfcauchy p: 0.0 D: nan
halflogistic p: 0.861779698542 D: 0.0269170250918
halfnorm p: 0.0196547930831 D: 0.0676373500658
hypsecant p: 5.24874010255e-07 D: 0.122585921974
invgamma p: 0.0 D: nan
invnorm p: 2.05302441714e-12 D: 0.1653403998
invweibull p: 0.0 D: nan
johnsonsb p: 0.000123301008122 D: 0.0980415299941
johnsonsu p: 0.187690615262 D: 0.0483085152879
laplace p: 6.4301079794e-08 D: 0.130794611581
logistic p: 2.0080315426e-06 D: 0.117035439077
loggamma p: 2.47024765088e-07 D: 0.125595005169
loglaplace p: 0.0 D: nan
lognorm p: 0.0 D: 0.244376114481
lomax p: 0.0 D: nan
maxwell p: 2.66340772692e-05 D: 0.105513802146
mielke p: 0.0 D: nan
nakagami p: 0.062823527118 D: 0.0584847713556
ncx2 p: 0.0 D: 0.202
nct p: 0.304057037747 D: 0.04306998817
pareto p: 0.0 D: nan
powerlaw p: 0.0 D: 0.312
powerlognorm p: 0.0 D: 0.244376111364
powernorm p: 2.69737565617e-09 D: 0.142287416118
rdist p: 0.0 D: 0.214
reciprocal p: 0.0 D: nan
rayleigh p: 2.32825345954e-05 D: 0.106144314494
rice p: 2.33073358471e-05 D: 0.106139337907
recipinvgauss p: 0.00103126062912 D: 0.0866200793693
semicircular p: 1.06979536341e-10 D: 0.153087213516
t p: 1.97532985635e-06 D: 0.117104968508
triang p: 7.32747196253e-15 D: 0.181385693511
truncexpon p: 7.42279948618e-09 D: 0.138723917087
truncnorm p: 0.0 D: nan
tukeylambda p: 1.59758457396e-06 D: 0.118
uniform p: 1.87294624254e-12 D: 0.165614214095
vonmises p: nan D: 1.05769878583e+28
wald p: 2.05302441714e-12 D: 0.1653403998
weibull_min p: 1.55989546051e-05 D: 0.108
weibull_max p: 0.0 D: 0.250852727712
wrapcauchy p: 0.0 D: nan
ksone p: 0.0 D: nan
kstwobign p: 0.0402335754919 D: 0.0621540114157And the winner is … have a look on line 39 … the half-logistic probability distribution, closely followed by genexpon (in line 28).
You can download the source-code at (git clone):
https://github.com/andre-dietrich/distribution-check
with the following command you can generate an example file:
$ python distribution_check.py --generateand run the test with:
$ python distribution_check.py --file example-halflogistic.datcheck out the other parameters with:
$ python distribution_check.py --help
Options:
-h, --help show this help message and exit
-f FILE, --file=FILE file with measurement data
-v, --verbose print all results immediately (default=False)
-t TOP, --top=TOP define amount of printed results (default=10)
-p, --plot plot the best result with matplotlib (default=False)
-i ITERATIVE, --iterative=ITERATIVE
define number of iterative checks (default=1)
-e EXCLUDE, --exclude=EXCLUDE
amount (in per cent) of exluded samples for each
iteration (default=10.0%)
-n PROCESSES, --processes=PROCESSES
number of process used in parallel (default=-1...all)
-d, --densities
-g, --generate generate an example fileenjoy 😉
